(Two Sigma/Digital learning transformation series
Some people are just not ready to learn a given topic, others need a lot of help -- and with that help can make a good "go" of it -- and some "breeze through" easily.
Why is that?
Where do intelligence and cognitive development fit in?
And, how does this affect the idea we have been examining, that by shifting how we go about teaching and learning, we can make a big difference to outcomes? (A difference that credibly can make a difference not only for our students, but for our region's prospects in the emerging high tech world.)
The second question is much easier to answer: the implicit assumption in Bloom's studies on the impact of mastery learning and 1:1 tutorials, etc, was that we were dealing with people who were reasonably "ready" for the new units of study in view.
Lev Vygotsky has a useful "window of opportunity" model that allows us to draw out a bit on what "readiness" to learn is, and so to open the door to looking at relevant issues about learning, intelligence, cognitive development etc etc:
 |
| Vygotsky's Zone of Proximal Development (ZPD) which shows what has been mastered, what can be learned with some help ("scaffolding") from More Knowledgeable Others [MKO's], what would need much help to be learned, and what could not reasonably be learned in the current period even with much help |
What this model does is it shows us how some students, given what they have already mastered, can easily progress, and why some will need a lot of structured help (live and/or "canned" from books, videos, web media etc), and why some will not be able to master new materials in the available time.
That brings up the organisation -- the architecture -- of Benjamin Bloom's Mastery learning curriculum approach:
That brings up the organisation -- the architecture -- of Benjamin Bloom's Mastery learning curriculum approach:
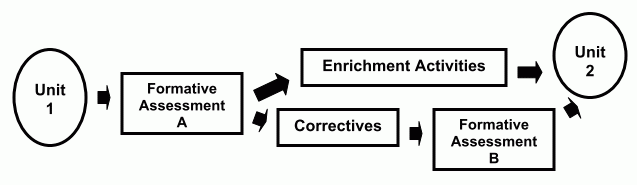 |
| Bloom's mastery learning approach uses small successive units [1 and 2], which have "formative assessment" modules [A and B] that allow for enrichment and corrective study, so that students master one stage before they move on to the next. This allows us to inject a degree of individualisation, interactivity, feedback and flexibility, but requires a considerable investment in developing the specific structure in light of the challenges that students may have and the opportunities for enrichment. |
Obviously, if a student is trying to operate beyond his or her window of learning opportunity -- zone of proximal development (ZPD) -- s/he is very likely to be frustrated and fail rather badly, even if there is a lot of help. Those who can only progress with considerable help -- "weak students" -- will be heavily dependent on the way a curriculum progresses, especially how it helps them find and fix gaps in their base of knowledge, or new gaps that emerge as the learning period progresses. The ones who have a strong base -- the "bright" or "gifted" students -- will easily learn with minimal support, but may then be held back as the class deals with the problems being encountered by "slower" students. That brings up the significance of "enrichment" and the need for individualisation at the high achievement end.
A subtlety here, is that when we construct assessments of learning, we may so emphasise recall and recipe based application to set-piece standard exercise problems, that at one level of study, students may seem to understand more than they do. Then, at the next level, where "real understanding" is actually needed to do serious analysis, creative designs and evaluations, they will predictably run into readiness problems.
In short, because of defects or inherent difficulties in how we assess students (whether as part of feedback and adjustment of the learning process or as a summing up certification), students can seem to be more ready to learn onward topics than they really are. And, it is tempting to subtly downgrade the way a course is delivered, to make it "easier" for students, creating problems for later or parallel units of study.
(BTW, this is why it is very important for an overall curriculum across several subjects and periods of study to be carefully structured so it is coherent and not too difficult for all but the "brightest.")
That brings up Richard Skemp's distinction between instrumental and what we could call insightful understanding (Skemp uses "relational"):
It was brought to my attention some years ago by Stieg Mellin-Olsen, of Bergen University, that there are in current use two meanings of this word. These he distinguishes by calling them ‘relational understanding’ and ‘instrumental understand-ing’. By the former is meant what I have always meant by understand-ing, and probably most readers of this article: knowing both what to do and why. Instrumental understanding I would until recently not have regarded as understanding at all. It is what I have in the past described as ‘rules without reasons’, without realising that for many pupils and their teachers the possession of such a rule, and ability to use it, was
why they meant by ‘understanding’ . . .
That is, one of the challenges we have is to understand understanding itself. For, when we need genuine insight to move forward, but only have a memorise- and- use- blindly- because- it- works level of actual learning, we are setting up trouble. Which sounds uncomfortably familiar.
Especially, in situations where that sort of "practical knowledge" level of instrumental understanding is "good enough for government work."
Boiling down, we can easily see a gap emerging between say O Level 4th and 5th form studies [Grades 10 - 11] and requisites for more sophisticated studies starting with A levels [6th form or Grades 12 - "13" the last being an effectively an advanced College level placement].
Sounds familiar?
It should.
How do we escape this trap?
The 2001 revision of benjamin Bloom's taxonomy of learning objectives for the cognitive [~ "academic"] domain, as presented as a table by Fisher of Oregon State University, will be helpful here:
| The Knowledge Dimension | The Cognitive Process Dimension | |||||
|---|---|---|---|---|---|---|
| Remember | Understand | Apply | Analyze | Evaluate | Create | |
| Factual Knowledge | List | Summarize | Classify | Order | Rank | Combine |
| Conceptual Knowledge | Describe | Interpret | Experiment | Explain | Assess | Plan |
| Procedural Knowledge | Tabulate | Predict | Calculate | Differentiate | Conclude | Compose |
| Meta-Cognitive Knowledge | Appropriate Use | Execute | Construct | Achieve | Action | Actualize |
Copyright (c) 2005 Extended Campus -- Oregon State University http://oregonstate.edu/instruct/coursedev/models/id/taxonomy/#table Designer/Developer - Dianna Fisher
In effect, we need to ensure that students are actually analysing, evaluating and creating, which requires that they be able to work with novel situations and topics. This is part of the valid reason for building independent research and projects in the curriculum. The challenge here, is that a lot of students will require "scaffolding" to help them do that, and we have to reckon with the evidence that only about 1/3 of adults in even "advanced"/ "developed" societies actually achieve Jean Piaget's formal operations stage of cognitive development. Unfortunately, this is the precise level required for full mastery of logical and mathematical reasoning:
 |
| Even in "advanced" countries, only a fairly small proportion of the population achieve Piaget's formal operations stage of development, perhaps up to 30 - 35% |
That brings up Piaget's model of how we come to understand, and onward, of how our cognitive abilities tend to develop, which he initially developed from his experience of working with young children as he realised that there are differences of kind in the ways children of different ages form and use ideas. As, at root, a biologist, he set his thinking in a biological context, where several stages emerge in succession as the child matures, and in part in response to the challenges of an environment. (This last becomes important to those who come after, especially for the transition to formal operations.)
First, some basic dynamics:
According to Piaget, two major principles guide intellectual growth and biological development: adaptation and organization. For individuals to survive in an environment, they must adapt to physical and mental stimuli. Assimilation and accommodation are both part of the adaptation process. Piaget believed that human beings possess mental structures that assimilate external events, and convert them to fit their mental structures. Moreover, mental structures accommodate themselves to new, unusual, and constantly changing aspects of the external environment.
Piaget's second principle, organization, refers to the nature of these adaptive mental structures. He suggests that the mind is organized in complex and integrated ways. The simplest level is the schema, a mental representation of some physical or mental action that can be performed on an object, event, or phenomenon.
Let us glance at a summary of Piaget's stages, adequate for our purposes of forming a rough-cut model for doing some practical curriculum transformation for the digital age, rather than getting into the gory details of an academic study of Piaget's thought and that of the Neo Piagetians such as Demitriou:
Piaget identified four stages in cognitive development:
- Sensorimotor stage (Infancy [~ 0 - 2 yrs]). In this period (which has 6 stages), intelligence is demonstrated through motor activity without the use of symbols. Knowledge of the world is limited (but developing) because its based on physical interactions / experiences. Children acquire object permanence at about 7 months of age (memory). Physical development (mobility) allows the child to begin developing new intellectual abilities. Some symbollic (language) abilities are developed at the end of this stage.
- Pre-operational stage (Toddler and Early Childhood [2 - 7 yrs]). In this period (which has two substages), intelligence is demonstrated through the use of symbols, language use matures, and memory and imagination are developed, but thinking is done in a nonlogical, nonreversable manner. Egocentric thinking predominates
- Concrete operational stage (Elementary and early adolescence [7 - 11 years]). In this stage (characterized by 7 types of conservation: number, length, liquid, mass, weight, area, volume), intelligence is demonstarted through logical and systematic manipulation of symbols related to concrete objects. Operational thinking develops (mental actions that are reversible). Egocentric thought diminishes.
- Formal operational stage (Adolescence and adulthood). In this stage, intelligence is demonstrated through the logical use of symbols related to abstract concepts. Early in the period there is a return to egocentric thought. Only 35% of high school graduates in industrialized countries obtain formal operations; many people do not think formally during adulthood.
There has been a debate on how much of this development is empirically well warranted, and on how much is socially influenced, etc. It suffices to know that this has shaped further thought, and has established the idea of emerging stages of capacity linked to how fast we can process information to meet challenges or opportunities, how we organise and manage the processing, how much we can store in a working register [1 or 2 up to about 7 "units"] and in short term memory, the connexion (if any) to underlying "plastic" general intelligence -- and about how much this can be shaped by environment and experience -- and more. As I recall, there is some report of chunks of long term storage of up to about 50,000 items, that form the basis for expert performance, etc.
An excerpt from Adey et al, in the face of an intense political debate tinged by class-elitism and racial prejudices etc. (which they argue, can be moulded by environment and learning experiences . . . ), may help:
[W]ithout re-introducing general cognitive ability into the educational discourse, efforts at theorizing educational goals, setting standards and conceptualizing assessment frameworks cannot be successful . . . .
If you ask teachers anywhere in the world what counts to them as a ‘clever’ or ‘smart’ response from a student, you get a remarkably consistent sets of characteristics (Adey, 2007). High in the lists of common answers are a set of essentially convergent abilities (‘thinks logically’, ‘applies knowledge from one context to another’, ‘demonstrates deep understanding of a concept’) and also a set of generally divergent abilities (‘creative’, ‘asks surprising questions’, ‘goes beyond the given’). These responses explicate professional, intuitive, experienced-based conceptions of general ability . . . .
[P]ractitioners’ conceptions of general ability always include features which require that the student make some sort of connection in their mind between, for example, one context and another, actuality and possibilities, or between data items such that a pattern is perceived. The professionals who are in the business of teaching and learning therefore see connectivity as a central characteristic of smart behaviour. ‘Connectivity’ here is used in the simple sense of the conscious or unconscious making of connections in the mind between one idea and another. In this sense, making comparisons, extrapolating, relating causes to effects, or the elucidation of any relationship between variables all involve connectivity . . . .
[The ideas and findings of recent researchers] converge to a common denominator . . . From the point of view of development, it reflects the brain’s and thus the mind’s increasing ability to construct and use goal-relevant and appropriate mental structures and skills and the responsiveness of the developing brain to environmental stimuli. From the differential point of view, it reflects the fact that differences between individuals in plasticity will eventually demonstrate themselves as differences in actual intellectual constructions and achievements.
In short, it is reasonable or at least a viable view to accept that there is an underlying general intelligence that supports both learning and performance, develops in a partly biologically grounded way and partly based on environment and experiences, which brings out the significance of education.
But there is no sufficiently solid warrant for the formerly dominant view that sees intelligence as a fixed, genetically determined entity that is often obvious and correlated with certain classes, races and sexes, that then warrants an education system based on filtering off the sheep from the goats. Unfortunately, the 11+ Common Entrance system of education was based on this former view, and -- quite disturbingly -- in turn Sir Cyril Burt's separated twins studies that seemed to ground it, were based on questionable statistical investigations involving apparently cooked numbers and some of the collaborators listed may not have existed or were not what they were represented as.
Yes, there is some evidence of general intelligence and there is some evidence of diversity of intelligence in major domains. Highly gifted and talented people can have surprising gaps in their capacities, and there are autistic savants who are otherwise severely retarded but can perform astonishing feats of say arithmetic. The overall evidence is complex and the literature is even more complex.
However, as a supplement to the zone of proximate development model in light of Piaget's genral stages, it is well worth drawing on a learning and development oriented model by Andreas Demetriou (who was not only a professor of education but at one point Cyprus' minister of education!):
 |
| Demetriou's model of developing conceptual schemes in domains of learning and capacity |
As I look on this diagram in general terms (what we really need for our immediate purposes):
1 --> I see a growing, transparent model of something like a tree-trunk, with a core and rings, some of which are segmented. It is worth noting on the visual-spatial skills involved in reading this model:
a: I can "see" with my mind's eye not only the three-dimensional tree trunk, but I can make it become coloured and transparent, i.e. I am moving from the projection to a three dimensional mental image. (Someone I discussed this with said how for her, it could "pop" out of the page for a moment, then it would collapse back into being simply lines on paper.)
b: I can see the three-dimensional model in a vague back and over the head position normally, but I can move it in front of me, rotate it, watch it grow or shrink, etc.
c: I can bring up other elements such as the Vygotsky window diagram or the Bloom taxonomy, and compare and make connexions. (But usually just to one or two such at a time. Beyond that, details get fuzzy, though I can zoom. I can suspend several fuzzy related diagrams then zoom in on each in succession.)
d: I can make up a mental movie, that seems to float in a chiaroscuro, black background world with vivid colours. I suspect the colours bear a suspicious resemblance to the palette of an LCD computer screen
e: I suspect that from this I can make a storyboard, and could either make a video animation, or could use the pattern to construct an interactive simulation, with help in the detailed coding.
f: As a related exercise, I think about how I struggled at first to understand how the inverting operational amplifier circuit worked. For this, I found it very helpful to get a sheet of paper and draw the diagram, then play out the calculation that yields the gain expression. That tells me a limit on my personal mental chalkboard. Here, courtesy Wiki [I feel too lazy to draw it this morning], is the inverter circuit, where the triangle is the amp, the lines are wires and the zig-zags are the resistors:
g: I then put the Bloom taxonomy next to it. Recalling and recognising and correctly placing the elements in the diagram was simple, and so was recalling that Ohm's law, the summing point restraints that say that the feedback network drives the voltage between the differential signal input terminals to zero, while the terminals do not draw any current. Here is a model of the idealised innards of the amp, also showing power supply terminals but leaving off offset and compensation terminals or the like:
h: I then saw that the derivation that moves from that to deriving the gain expression requires Bloom's analysis. That analysis requires significant algebra and ability to interpret electronic circuit symbols in light of a graphical-algebraic model. So, probably there were weaknesses there when I first met this diagram and the related analysis.
i: Going on to understand how to "take out" the idealisations requires evaluation of the weaknesses involved and a fair understanding of the innards of the op amp, which is usually based on some sort of long tail pair differential amplifier driving gain and power stages. (The linked diagram is for the classic 741.) In Integrated Circuit (IC) op amps -- and to follow the pinouts of the chip package is itself a little exercise in several levels of reasoning -- there are often current mirrors, which requires some understanding of IC creation techniques. The realities of these techniques drive the behaviour of real world as opposed to idealised op amps. (This in turn leads to the value of chopper stabilisation and other modifications that improve behaviour.)
j: I then could generalise the derivation, to deduce integrators, differentiators, logging and antilogging amps, filters, oscillators etc. Real world considerations then ground design of practical circuits that have to work in the practical world, e.g. I remember being puzzled at first by how we move from having a ratio of resistances etc to a good practical value from the various series of standard values. (As a couple of rules of thumb, a reasonably high resistance will not load input transducers or stages over-much, but too high a resistance brings to bear noise and parasitic filter effects that can undermine a design. If you want precision, count on having to pay for high quality, low tolerance components. Don't expect to find wound components that will be precise. But, there are op amp circuits that can simulate their behaviour; if you absolutely need such in an instrument.)
k: This shows me that capacities from earlier learning do make a difference to how one can progress in a new area, and that analysis and evaluation do often precede design or genuine creation. (Canned cookbook designs based on following the usual cookbooks or magazines etc don't count. Of course, all too often often cookbook designs may not work with the particular cluster of tolerances in a given circuit and it has to be fiddled with through debugging or troubleshooting.)
2 --> Back to the Demetriou diagram. There are four main stages of growth as can be seen on the left. We start with Piaget's sensorimotor stage then we begin to "see" relationships, reaching stage 2. This is also the stage where we first begin to use and develop symbols and related concepts and organised systems of concepts etc [i.e. Piaget's schemes], especially through language.
3 --> Three-dimensional spatial thinking and abstract thinking follow, at stages 3 and 4. It is obvious that it is much easier to deal with these concretely with physical models at first, then use computer simulations to gradually build up mental visualisation capability. After that, sketches on paper etc can be mentally transformed into the mind's "Star Trek 3-D holodeck"! (H'mm: watching star trek as homework . . . )
4 --> The squiggles in the right hand wedge on the disgram show the emergence of Piaget's schemas, connected networks of concepts etc.
5 --> At first level, concepts are abstracted from experiences, and become a basis for further abstractions to form a network.
6 --> When our schemes are accurate and useful models we can say we have formed good and insightful understandings.
7 --> As a bonus, we have a handle on why models, simulations and theories are so important in science, and a glimpse onward at the significance of worldviews.
6 --> When our schemes are accurate and useful models we can say we have formed good and insightful understandings.
7 --> As a bonus, we have a handle on why models, simulations and theories are so important in science, and a glimpse onward at the significance of worldviews.
Much of the educational challenge before us, we can now see, comes in the need to develop new stages of ability to form abstractions, and thus from the intersection of the different wedges with Vygotsky's zone of proximal development. For, it is gaps in the underlying framework of knowledge, understanding and skills that so often lead to failure as onward stages of learning call on the higher order learning that Bloom identified, and which may well not be there.
So, we have scoped out a picture of areas we need to work on if our curriculum transformation efforts are to succeed.
The creation of interactive supportive learning structures with the ability to adapt to the needs of individual learners, also emerges as a vital capacity for educational transformation. This points straight to the importance of the multimedia, web connected computer as a major educational instrument. Indeed, maybe many of the more knowledgeable others in the learning activity space will be coming to us digitally!
The creation of interactive supportive learning structures with the ability to adapt to the needs of individual learners, also emerges as a vital capacity for educational transformation. This points straight to the importance of the multimedia, web connected computer as a major educational instrument. Indeed, maybe many of the more knowledgeable others in the learning activity space will be coming to us digitally!

